Conventions

States and Bases

Bases

A basis refers to a set of two eigenstates. The transition between these two states is said to be addressed by a channel that targets that basis. Namely:

Basis	Eigenstates	Channel type
ground-rydberg	\(|g\rangle,~|r\rangle\)	Rydberg
digital	\(|g\rangle,~|h\rangle\)	Raman
XY	\(|0\rangle,~|1\rangle\)	Microwave

Qutrit state

The qutrit state combines the basis states of the ground-rydberg and digital bases, which share the same ground state, \(|g\rangle\). This qutrit state comes into play in the digital approach, where the qubit state is encoded in \(|g\rangle\) and \(|h\rangle\) but then the Rydberg state \(|r\rangle\) is accessed in multi-qubit gates.

The qutrit state’s basis vectors are defined as:

\[ |r\rangle = (1, 0, 0)^T,~~|g\rangle = (0, 1, 0)^T, ~~|h\rangle = (0, 0, 1)^T. \]

Qubit states

Caution

There is no implicit relationship between a state’s vector representation and its associated measurement value. To see the measurement value of a state for each measurement basis, see Initial State and Measurement Conventions .

When using only the ground-rydberg or digital basis, the qutrit state is not needed and is thus reduced to a qubit state. This reduction is made simply by tracing-out the extra basis state, so we obtain

• ground-rydberg: \(|r\rangle = (1, 0)^T,~~|g\rangle = (0, 1)^T\)

• digital: \(|g\rangle = (1, 0)^T,~~|h\rangle = (0, 1)^T\)

On the other hand, the XY basis uses an independent set of qubit states that are labelled \(|0\rangle\) and \(|1\rangle\) and follow the standard convention:

• XY: \(|0\rangle = (1, 0)^T,~~|1\rangle = (0, 1)^T\)

Multi-partite states

The combined quantum state of multiple atoms respects their order in the Register. For a register with ordered atoms (q0, q1, q2, ..., qn), the full quantum state will be

\[ |q_0, q_1, q_2, ...\rangle = |q_0\rangle \otimes |q_1\rangle \otimes |q_2\rangle \otimes ... \otimes |q_n\rangle \]

Note

The atoms may be labelled arbitrarily without any inherent order, it’s only the order with which they are stored in the Register (as returned by Register.qubit_ids) that matters .

State Preparation and Measurement

Initial State and Measurement Conventions

Basis	Initial state	Measurement
ground-rydberg	\(|g\rangle\)	\(|r\rangle \rightarrow 1\) \(|g\rangle,|h\rangle \rightarrow 0\)
digital	\(|g\rangle\)	\(|h\rangle \rightarrow 1\) \(|g\rangle,|r\rangle \rightarrow 0\)
XY	\(|0\rangle\)	\(|1\rangle \rightarrow 1\) \(|0\rangle \rightarrow 0\)

Measurement samples order

Measurement samples are returned as a sequence of 0s and 1s, in the same order as the atoms in the Register and in the multi-partite state.

For example, a four-qutrit state \(|q_0, q_1, q_2, q_3\rangle\) that’s projected onto \(|g, r, h, r\rangle\) when measured will record a count to sample

• 0101, if measured in the ground-rydberg basis

• 0010, if measured in the digital basis

Hamiltonians

Tip

This section uses formulas that rely on the Indexed Operator notation.

Independently of the mode of operation, the Hamiltonian describing the system can be written as

\[ H(t) = \sum_i \left (H^D_i(t) + \sum_{j<i}H^\text{int}_{ij} \right), \]

where \(H^D_i\) is the driving Hamiltonian for atom \(i\) and \(H^\text{int}_{ij}\) is the interaction Hamiltonian between atoms \(i\) and \(j\). Note that, if multiple basis are addressed, there will be a corresponding driving Hamiltonian for each transition.

Driving Hamiltonian

The driving Hamiltonian describes the coherent excitation of an individual atom between two energies levels, \(|a\rangle\) and \(|b\rangle\), with Rabi frequency \(\Omega(t)\), detuning \(\delta(t)\) and phase \(\phi(t)\).

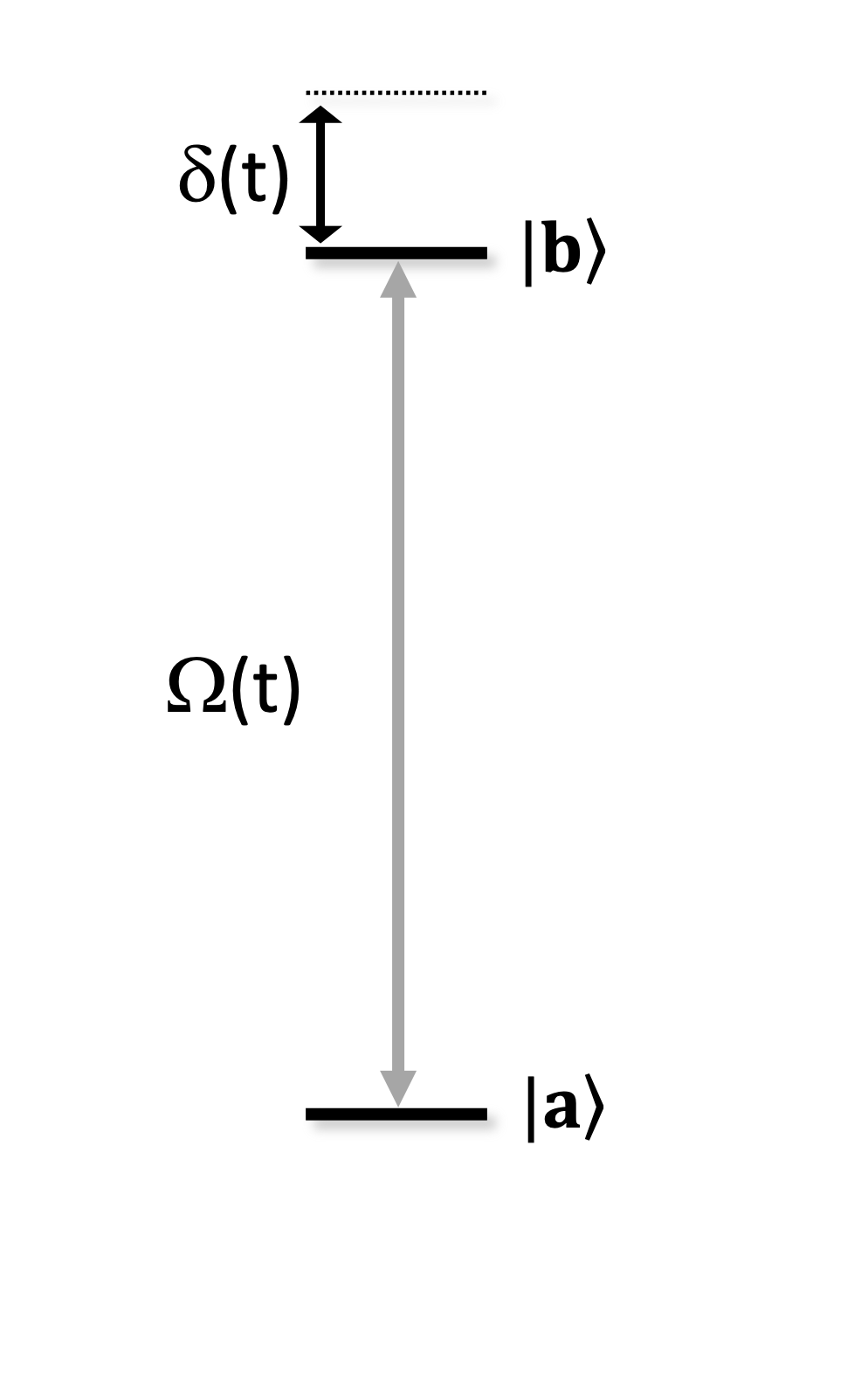
The coherent excitation is driven between a lower energy level, \(|a\rangle\), and a higher energy level, \(|b\rangle\), with Rabi frequency \(\Omega(t)\) and detuning \(\delta(t)\).

Warning

In this form, the Hamiltonian is independent of the state vector representation of each basis state, but it still assumes that \(|b\rangle\) has a higher energy than \(|a\rangle\).

\[ H^D(t) / \hbar = \frac{\Omega(t)}{2} e^{-i\phi(t)} |a\rangle\langle b| + \frac{\Omega(t)}{2} e^{i\phi(t)} |b\rangle\langle a| - \delta(t) |b\rangle\langle b| \]

Pauli matrix form

A more conventional representation of the driving Hamiltonian uses Pauli operators instead of projectors. However, this form now depends on the state vector definition of \(|a\rangle\) and \(|b\rangle\).

Pulser’s state-vector definition

In Pulser, we consistently define the state vectors according to their relative energy. In this way we have, for any given basis, that

\[ |b\rangle = (1, 0)^T,~~|a\rangle = (0, 1)^T \]

Thus, the Pauli and excited state occupation operators are defined as

\[\begin{split} \hat{\sigma}^x = |a\rangle\langle b| + |b\rangle\langle a|, \\ \hat{\sigma}^y = i|a\rangle\langle b| - i|b\rangle\langle a|, \\ \hat{\sigma}^z = |b\rangle\langle b| - |a\rangle\langle a| \\ \hat{n} = |b\rangle\langle b| = (1 + \sigma_z) / 2 \end{split}\]

and the driving Hamiltonian takes the form

\[ H^D(t) / \hbar = \frac{\Omega(t)}{2} \cos\phi(t) \hat{\sigma}^x - \frac{\Omega(t)}{2} \sin\phi(t) \hat{\sigma}^y - \delta(t) \hat{n} \]

Alternative state-vector definition

Outside of Pulser, the alternative definition for the basis state vectors might be taken:

\[ |a\rangle = (1, 0)^T,~~|b\rangle = (0, 1)^T \]

This changes the operators and Hamiltonian definitions, as rewriten below with highlighted differences.

\[\begin{split} \hat{\sigma}^x = |a\rangle\langle b| + |b\rangle\langle a|, \\ \hat{\sigma}^y = \textcolor{red}{-}i|a\rangle\langle b| \textcolor{red}{+}i|b\rangle\langle a|, \\ \hat{\sigma}^z = \textcolor{red}{-}|b\rangle\langle b| \textcolor{red}{+} |a\rangle\langle a| \\ \hat{n} = |b\rangle\langle b| = (1 \textcolor{red}{-} \sigma_z) / 2 \end{split}\]

\[ H^D(t) / \hbar = \frac{\Omega(t)}{2} \cos\phi(t) \hat{\sigma}^x \textcolor{red}{+}\frac{\Omega(t)}{2} \sin\phi(t) \hat{\sigma}^y - \delta(t) \hat{n} \]

Note

A common case for the use of this alternative definition arises when trying to reconcile the basis states of the ground-rydberg basis (where \(|r\rangle\) is the higher energy level) with the computational-basis state-vector convention, thus ending up with

\[ |0\rangle = |g\rangle = |a\rangle = (1, 0)^T,~~|1\rangle = |r\rangle = |b\rangle = (0, 1)^T \]

Interaction Hamiltonian

The interaction Hamiltonian depends on the states involved in the sequence. When working with the ground-rydberg and digital bases, atoms interact when they are in the Rydberg state \(|r\rangle\):

\[ H^\text{int}_{ij} = \frac{C_6}{R_{ij}^6} \hat{n}_i \hat{n}_j \]

where \(\hat{n}_i = |r\rangle\langle r|_i\) (the projector of atom \(i\) onto the Rydberg state), \(R_{ij}^6\) is the distance between atoms \(i\) and \(j\) and \(C_6\) is a coefficient depending on the specific Rydberg level of \(|r\rangle\).

On the other hand, with the two Rydberg states of the XY basis, the interaction Hamiltonian takes the form

\[ H^\text{int}_{ij} = \frac{C_3}{R_{ij}^3} (\hat{\sigma}_i^{+}\hat{\sigma}_j^{-} + \hat{\sigma}_i^{-}\hat{\sigma}_j^{+}) \]

where \(C_3\) is a coefficient that depends on the chosen Ryberg states and

\[ \hat{\sigma}_i^{+} = |1\rangle\langle 0|_i,~~~\hat{\sigma}_i^{-} = |0\rangle\langle 1|_i \]

Note

The definitions given for both interaction Hamiltonians are independent of the chosen state vector convention.

Notation

Indexed Operator

Whenever an arbitrary operator is written with an index (typically \(i\) or \(j\)), e.g. \(\hat{O}_i\), it is implicit that \(\hat{O}\) is applied only to qudit \(i\) while the rest of the qudits are applied the identity operator, \(\hat{I}\). Put another way,

\[ \hat{O}_i = \underset{(1)}{\hat{I}} \otimes \underset{(2)}{\hat{I}} \otimes ... \otimes\ \underset{(i)}{\hat{O}}\ \otimes ... \otimes \underset{(N)}{\hat{I}},\]

where \(1 \leq i \leq N\).

This notation is extendable to multiple indices. Take for instance the case with two indices, \(\hat{O}_{ij}\) – here, \(\hat{O}\) is a two-qudit operator. A good example is the interaction Hamiltonian in the ground-rydberg basis, which we write as

\[H^\text{int}_{ij} = \frac{C_6}{R_{ij}^6} \hat{n}_i \hat{n}_j = \frac{C_6}{R_{ij}^6} \left( \underset{(1)}{\hat{I}} \otimes ... \otimes \ \underset{(j)}{\hat{n}}\ \otimes ... \otimes \ \underset{(i)}{\hat{n}} \ \otimes ... \otimes \underset{(N)}{\hat{I}}\right),\]

where \(1 \leq j < i \leq N\).

Note that, generally, we cannot write \(\hat{O}_{ij}\) in the form used above because \(\hat{O}\) might not be separable in a tensor product of two single-qudit operators, but the operator is valid nonetheless.