Quickstart: The Rydberg Blockade

The following walkthrough highlights some of Pulser’s core features and uses them to display a crucial physical effect for neutral atom devices: the Rydberg blockade. Bear in mind that it is not meant to be a comprehensive step-by-step guide on how to use Pulser, but rather a showcase of Pulser in action.

For a more detailed introduction to Pulser, check the tutorials on Pulse Sequence Creation and Simulation of Sequences. To better understand neutral atom devices and how they serve as quantum computers and simulators, check the pages in Quantum Computing with Neutral Atoms.

Pulser’s main features

import matplotlib.pyplot as plt
import numpy as np
import pulser
from pulser_simulation import QutipEmulator

With pulser, it is easy to define a Register consisting of any arrangement of atoms in a quantum processor. For example, we can generate a register with hexagonal shape:

layers = 3
reg = pulser.Register.hexagon(layers)
reg.draw(with_labels=False)

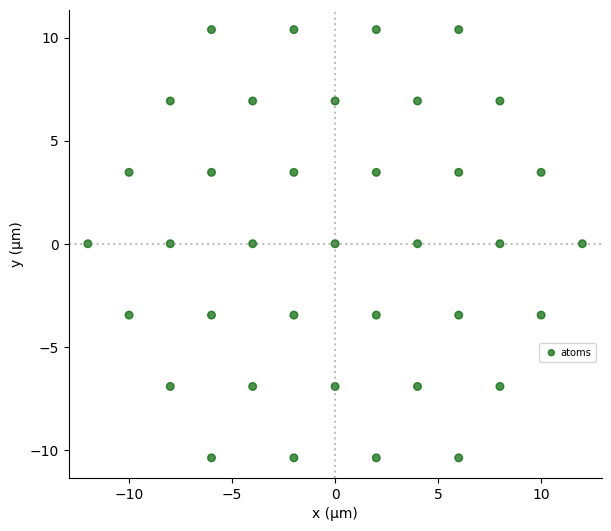
In fact, we can place the atoms in arbitrary positions by specifying the positions of each one. As an exotic example, here is a picture of the Gioconda as a register of neutral atoms made using Pulser:

It is also simple to create and design a Pulse that will act on the atom array:

duration = 1000  # Typical: ~1 µsec
pulse = pulser.Pulse(
    amplitude=pulser.BlackmanWaveform(duration, np.pi),
    detuning=pulser.RampWaveform(duration, -5.0, 10.0),
    phase=0,
)
pulse.draw()

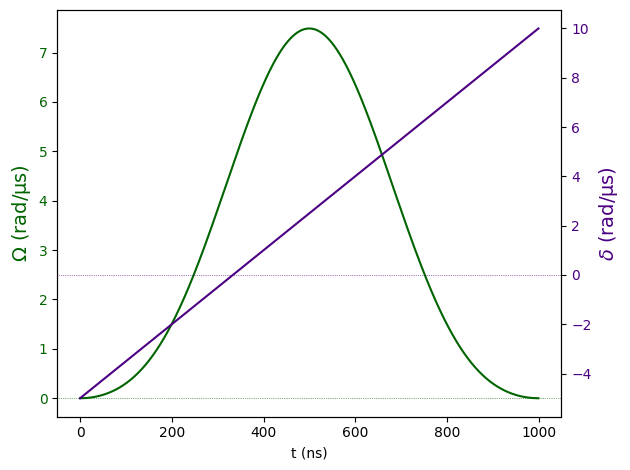
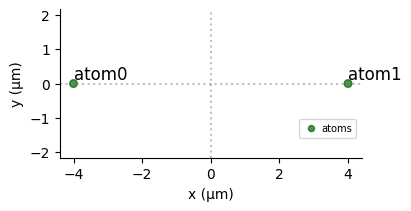
Each pulse acts on a set of atoms at a certain moment of time. The entire Sequence is stored by Pulser and can then be either simulated or sent to a real device. Below is the example of a sequence sending the same \(\pi\)-pulse to two atoms, sequentially, using the same channel.

reg = pulser.Register.rectangle(1, 2, spacing=8, prefix="atom")
reg.draw()

pi_pulse = pulser.Pulse.ConstantDetuning(
    pulser.BlackmanWaveform(duration, np.pi), 0.0, 0.0
)

seq = pulser.Sequence(reg, pulser.DigitalAnalogDevice)

seq.declare_channel("ryd", "rydberg_local", "atom0")

seq.add(pi_pulse, "ryd")
seq.target("atom1", "ryd")
seq.add(pi_pulse, "ryd")

seq.draw()

Probing the Rydberg Blockade Mechanism

Rydberg atoms are a prominent architecture for exploring condensed matter physics and quantum information processing. For example, one can use Pulser to write a sequence of succesive \(\pi\)-pulses on a two atom system, each one coupling the atom to its excited Rydberg state. This will allow us to study the Rydberg Blockade effect, using the dedicated pulser_simulation library:

The presence of the van der Waals interaction when both atoms are in the Rydberg state, prevents the collective ground state \(|gg\rangle\) to couple to \(|rr\rangle\), which is shifted out of resonance.

The Hamiltonian for the two-atom system can be written as:

\[H = \frac{\hbar \Omega_1(t)}{2} \sigma_1^x + \frac{\hbar \Omega_2(t)}{2} \sigma_2^x + U n_1n_2\]

We shall explore this blockade by changing the interatomic distance \(R\):

data = []
distances = np.linspace(6.5, 14, 7)

r = [1, 0]  # |r>
rr = np.kron(r, r)  # |rr>
occup = [np.outer(rr, np.conj(rr))]  # |rr><rr|

for i, R in enumerate(distances):
    # Atom Register and Device
    reg = pulser.Register.rectangle(1, 2, spacing=R, prefix="atom")

    # Pulse Sequence
    seq = pulser.Sequence(reg, pulser.DigitalAnalogDevice)
    seq.declare_channel("ryd", "rydberg_local", "atom0")
    seq.add(pi_pulse, "ryd")
    seq.target("atom1", "ryd")
    seq.add(pi_pulse, "ryd")

    sim = QutipEmulator.from_sequence(seq)

    res = sim.run()  # Returns a SimulationResults instance
    data.append(
        res.expect(occup)[0]
    )  # Get expectation value for the occupation operator
print("...Simulation Complete!")

...Simulation Complete!

We plot the results

for i, R in enumerate(distances):
    plt.plot(data[i], label=f"R={R}")
    plt.xlabel("Time (ns)", fontsize=14)
    plt.ylabel(r"Occupation of $|rr\rangle$", fontsize=14)
    plt.legend()

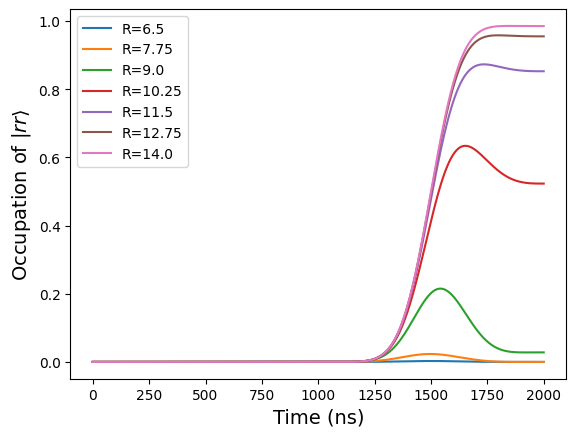
Notice how the occupation of \(|rr\rangle\) is suppressed for decreasing \(R\). This means that, up until a certain distance between the two atoms (called the Rydberg blockade radius), the fact that atom0 was first excited to the Rydberg state prevents atom1 from being excited to the same state with the same pulse, i.e. atom0 blockades the excitation of atom1 to the Rydberg state.

This conditional excitation of one atom depending on the state of another closely resembles that of a controlled gate in a quantum circuit. In fact, for neutral atom devices, the Rydberg blockade mechanism is the key behind entanglement generation between atoms.

You can find many more details about Pulser, its features and the neutral atom device architecture in this documentation and in the Tutorials.